Построить любую крышу не так просто, как кажется. А если хочется, чтобы она была надежной, прочной и не боялась различных нагрузок, то предварительно, еще на этапе проектирования, нужно произвести немало расчетов. И они будут включать в себя не только количество материалов, используемых для монтажа, но и определение углов наклона, площади скатов и т. д. Как рассчитать угол наклона крыши правильно? Именно от этого значения во многом будут зависеть и остальные параметры этой конструкции.
Как рассчитать угол наклона крыши
Почему это важно?
Проектирование и строительство любой кровли – всегда очень важное и ответственное дело. Особенно, если речь идет о кровле жилого дома или сложной по форме крыше. Но даже обычная односкатная, устанавливаемая на невзрачном сарайчике или гараже, точно так же нуждается в проведении предварительных расчетов.
Проект крыши
Если заранее не определить угол наклона кровли, не выяснить, какую оптимальную высоту должен иметь конек, то велик риск построить такую кровлю, которая рухнет после первого же снегопада, или все отделочное покрытие с нее будет сорвано даже умеренным по силе ветром.
Расчет угла наклона крыши
Также угол наклона кровли будет значительно влиять на высоту конька, на площадь и габариты скатов. В зависимости от этого можно будет более точно рассчитать количество требуемых для создания стропильной системы и отделки материалов.
Конек – важная часть стропильной системы
Цены на различные виды кровельных коньков
Конек кровельный
Как выбирают оптимальный угол проектировщики
Расчеты делаются на основании СНиП 2.01.07-85. Размещаемые нормы используются во время расчетов с учетом постоянно действующих, временных и особых нагрузок и их различных сочетаний.
СНиП 2.01.07-85. Файл PDF откроется в новой вкладке
Какие нагрузки принимаются во внимание при определении угла наклона крыши
Нагрузки делятся на несколько категорий в зависимости от продолжительности их воздействия: длительные, кратковременные и особые.
Длительные (постоянные) нагрузки на стропильную систему
- . К ним относится вес кровельных материалов, утеплителей, деревянных элементов стропильной конструкции. К этой категории следует относить нагрузки, возникающие вследствие тепловых расширений и изменений линейных размеров из-за изменений показателей относительной влажности пиломатериалов. Нормативные изменения температур определяются по формулам отдельно для отапливаемых и неотапливаемых помещений. Вес снегового покрова также считается длительной нагрузкой на стропильную систему и в обязательном порядке принимается во внимание во время определения оптимального угла наклона стропильных ног.
Нагрузка на стропильную систему
Снеговые нагрузки считаются длительными и принимаются в расчет
Ветровые нагрузки на крышу
В числе особых нагрузок — землетрясения и стихийные бедствия
Во время определения угла наклона крыши учитывается максимально возможное сочетание нагрузок. Оба эти параметра оказывают влияние на толщину и длину стропильных ног. Расчет стропильной системы и угла наклона скатов делается по предельным состояниям с учетом всех неблагоприятных факторов.
Максимальные прогибы и перемещение стропильных ног регламентируются без зависимости от их линейных размеров и не должны приводить к частичной разгерметизации крыши. Ко всем типам крыш, вне зависимости от угла наклона, выдвигаются такие условия:
- должна гарантироваться безопасная эксплуатация зданий;
- целостность конструкции не может нарушаться даже во время кратковременных пиковых нагрузок;
- внешний вид крыши не должен изменяться весь период эксплуатации.
Стропильная система должна выдерживать пиковые нагрузки без деформаций
При этом каждое требование должно выполняться вне зависимости от других. Предельные значения прогиба стропил ограничиваются с учетом эксплуатационных характеристик кровельных материалов. Если нормативные значения не оказывают заметного влияния на внешний вид, то они не корректируются.
Практический совет. Намного проще целостность кровельного пирога крыши обеспечивать не за счет увеличения прочности стропильной системы, а за счет использования специальных конструктивных компенсаторов.
Компенсатор усадки, скользящая опора
Единицы измерения
Вспоминая геометрию, которую каждый изучал в школе, можно с уверенностью заявить, что угол наклона крыши измеряется в градусах. Однако в книгах, посвященных строительству, а также в различных чертежах можно встретить и другой вариант – угол указан в процентах (тут имеется ввиду соотношение сторон).
В целом, углом наклона ската является угол, который образован двумя пересекающимися плоскостями – перекрытием и непосредственно скатом крыши. Он может быть только острым, то есть лежать в диапазоне 0-90 градусов.
Малый наклон скатов
На заметку! Очень крутые скаты, угол наклона которых составляет более 50 градусов, встречаются крайне редко в чистом виде. Обычно они используются только при декоративном оформлении крыш, могут присутствовать в мансардах.
Что касается измерения углов кровли в градусах, то тут все просто – эти знания есть у каждого, изучавшего в школе геометрию. Достаточно набросать схему кровли на бумаге и при помощи транспортира определить угол.
Выбор кровельного материала в зависимости от наклона крыши
Что касается процентов, то тут необходимо знать высоту конька и ширину здания. Первый показатель делится на второй, а полученное значение умножается на 100%. Таким образом, можно вычислить процентное соотношение.
На заметку! При процентном соотношении 1 обычный градус наклона равен 2,22%. То есть скат с углом 45 обычных градусов равен 100%. А 1 процент – это 27 угловых минут.
Таблица значений — градусы, минуты, проценты
Что такое уклон в процентах
Стоит поговорить об угле наклона скатов в процентах. Само понятие «угол наклона в процентах» технически неграмотное и используется только теми, кто сам ничего не строит.
Важно. Все запилы стропильных ног даются в градусах, во время сборки стропильной системы никто процентами не пользуется. Тем более что не существует измерительных инструментов, измеряющих углы в процентах. Есть специальные таблицы перевода процентов в углы, но об этом немного позже.
Рассмотрим данные определения на практике. Допустим, угол наклона скатов равняется 30%. Что это значит? Это значит, что высота конька крыши составляет 30% половины ширины здания. Для расчетов будем пользоваться тем же треугольником.
Прямоугольный треугольник
Процент наклона рассчитывается по формуле (см. рисунок ниже).
Процент наклона
Где:
- a – высота конька;
- b – половина ширины строения.
Что такое 30% и как смотрится крыша с таким процентным отношением представить себе очень трудно. Для того чтобы конвертировать эту величину в градусы следует воспользоваться специальной таблицей. С ее помощью узнаем, что 30% значит, что угол наклона ската кровли равняется примерно 16,5°. Дело в том, что для 16° процентное соотношение равняется 28,7%, а для 17° этот параметр составляет 30,5%. Если мастер знает, что угол уклона ската примерно 16,5°, то он без труда может представить внешний вид и геометрию крыши, рассчитать линейные размеры стропильных ног, вертикальных опор кровли, размеры мауэрлата. Как такие расчеты делаются, если есть данные наклона в процентах?
Примеры использования угла наклона в процентах
Расчет параметров стропильной системы с помощью процентного соотношения высоты конька и половины ширины строения делается при помощи калькулятора.
Имея начальную формулу, далее расчеты строятся с использованием элементарных арифметических уравнений. Для начала нужно немного преобразовать формулу.
Начальная формула
В данном случае X – процентное отношение наклона кровли, как мы договорились, для примера возьмем 30%. Эта величина известна и задается во время расчетов.
Для предварительных расчетов следует немного преобразовать формулу в такой вид (см. рисунок ниже).
Преобразованная формула
Теперь определяем по отдельности значения a и b.
Значение а
Значение b
Напомним, что:
- a – высота стропильной системы,
- b – половина ширины здания, а
- X – процент наклона ската.
Процент нам известен, для дальнейших расчетов понадобится замерить или высоту стропильной системы, или половину ширины здания. В связи с тем, что намного легче узнать второе значение, замерим его.
К примеру. Ширина здания 8 метров, соответственно, половина равняется 4 метра (b=4 м).
Узнаем высоту стропильной системы (см. рисунок ниже).
Узнаем высоту стропильной системы
Высота стропильной системы 1,2 метра, угол наклона мы узнали из таблицы, он равняется примерно 16,5°.
Далее нам следует рассчитать длину стропильной ноги без карнизного свеса. Идти можно двумя путями.
Первый. Используя теорему Пифагора, где c – длина стропилины.
Теорема Пифагора
Соответственно, значение с можно представить формулой на иллюстрации ниже.
Формула длины гипотенузы
Пример расчета (см. картинку ниже).
Пример расчета
Второй. Используя тригонометрические функции. Как мы уже выше указывали, расчет длины стропилины можно делать по формуле ниже.
Расчет длины стропилины
Все данные у нас есть, угол наклона 16,5°, половина ширины здания 4 м.
Пример выполнения расчета
По длине стропилины есть небольшие различия. Это объясняется тем, что угол наклона был выбран приблизительно.
Какие факторы влияют на угол наклона?
На угол наклона любой кровли влияет очень большое число факторов, начиная от пожеланий будущего владельца дома и заканчивая регионом, где дом будет располагаться. При расчете важно учитывать все тонкости, даже те, что на первый взгляд кажутся незначительными. В один прекрасный момент они могут сыграть свою роль. Определять подходящий угол наклона крыши следует, зная:
- виды материалов, из которых будет строиться пирог кровли, начиная от стропильной системы и заканчивая внешней отделкой;
- условия климата в данной местности (ветровая нагрузка, преобладающее направление ветров, количество осадков и т. д.);
- форму будущего строения, его высоту, дизайн;
- назначение строения, варианты использования чердачного помещения.
Что влияет на угол наклона кровли
В тех регионах, где отмечена сильная ветровая нагрузка, рекомендуется строить крышу с одним скатом и небольшим углом наклона. Тогда при сильном ветре у кровли больше шансов устоять и не быть сорванной. Если же для региона характерно большое количество осадков (снега или дождя), то скат лучше делать более крутым – это позволит осадкам скатываться/стекать с кровли и не создавать дополнительной нагрузки. Оптимальный уклон односкатной кровли в ветреных регионах варьируется в пределах 9-20 градусов, а там, где выпадает много осадков – до 60 градусов. Угол 45 градусов позволит не учитывать снеговую нагрузку в целом, но давление ветра в этом случае на крышу будет в 5 раз больше, чем на кровлю с наклоном всего 11 градусов.
На заметку! Чем больше параметры уклона крыши, тем большее количество материалов потребуется для ее создания. Стоимость увеличивается минимум на 20%.
Частота обрешетки для разных кровельных материалов
Зачем нужно знать уклон кровли
Без точного понимания этого вопроса невозможно разобраться с уклонами в градусах и процентах. На что влияет уклон скатов?
| Параметр кровли | Влияние на строительство крыши |
Вид кровельного материала | Каждый кровельный материал имеет ограничения по минимальному углу наклона. К примеру, на плоских крышах (угол наклона менее 10°) можно использовать только рулонные кровельные материалы, для штучной черепицы минимальный угол наклона 15° и т. д. Кроме того, от этого параметра зависит величина нахлеста гидроизоляции и кровельных материалов. |
| Ветровые и снеговые усилия | Чем больше угол наклона, тем меньше снеговые нагрузки на стропильную систему. С ветровыми нагрузками все сложнее. При небольших уклонах скатов во время сильных порывов ветра на них действует подъемная сила, если угол наклона увеличивается, то появляется опрокидывающая сила. Такое изменения нагрузок требует внимательного подхода во время проектирования и расчета стропильной системы. |
Расход материалов | Чем больше угол наклона – тем больше площадь скатов, перекрывающих план строения. Соответственно, увеличивается и расход кровельных материалов. К примеру, при уклоне скатов в 60° расход материалов вдвое больше, чем во время перекрытия строения плоской односкатной кровлей. |
Как видно из таблицы, угол наклона скатов крыши – один из самых важных технических параметров стропильной системы дома. На него обращают внимание с самого начала изготовления проекта строения.
Углы скатов и кровельные материалы
Не только климатические условия будут оказывать значительное влияние на форму и угол скатов. Немаловажную роль играют и используемые для строительства материалы, в частности – покрытие крыш.
Монтаж профилированного листа для кровли
Таблица. Оптимальные углы наклона скатов для кровель из различных материалов.
| Вид материала | Угол ската, градусы |
| Профнастил (металл) | 12 |
| Металлочерепица | 14-25 |
| Рубероид в зависимости от количества слоев | 2-15 |
| Шифер | 20-35 |
| Штучный материал типа кровельных камней и черепицы | 22-25 |
| Мягкая черепица | Минимум 11 |
На заметку! Чем меньше показатель наклона кровли, тем меньший шаг используется при создании обрешетки.
Рассчитываем угол наклона скатов
Цены на металлочерепицу
Металлочерепица
Оптимальный угол наклона двухскатной крыши
Угол правильной двускатной крыши лежит в пределах 20°-45°, что соответствует разбросу значений свойств материала и усредненных климатических параметров.
Следует иметь в виду, что рекомендуемые значения могут быть непригодны для данной местности или проекта, поэтому всякий раз надо рассчитывать угол двускатной крыши по конкретным имеющимся данным.
Угол наклона двухскатной крыши — важный показатель, влияющий на долговечность и целостность всей постройки, и относиться к нему как ко второстепенному фактору нельзя.
Учет всех возможных нагрузок, как постоянных, так и разовых экстремальных, поможет обеспечить сохранность и комфорт вашего дома.
Более точные значения выбираются исходя из таких факторов, как::
- Назначение чердака.
- Используемое кровельное покрытие.
- Климатические условия.
Оптимальный угол наклона двускатной крыши
Высота конька тоже зависит от угла ската
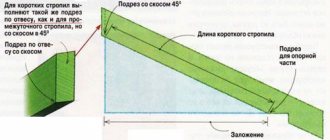
При расчетах любой кровли за ориентир всегда берется прямоугольный треугольник, где катеты – это высота ската в верхней точке, то есть в коньке или же переходе нижней части всей системы стропил в верхнюю (в случае с мансардными кровлями), а также проекция длины конкретного ската на горизонталь, которая представлена перекрытиями. Здесь есть только одна постоянная величина – это длина крыши между двумя стенами, то есть длина пролета. Высота коньковой части будет меняться в зависимости от угла наклона.
Высота конька может меняться в зависимости от угла наклона
Спроектировать кровлю помогут знания формул из тригонометрии: tgA = H/L, sinA = H/S, H = LхtgA, S = H/sinA, где А – это угол ската, Н – высота кровли к области конька, L – ½ всей длины пролета кровли (при двухскатной крыше) либо вся длина (в случае односкатной кровли), S – длина самого ската. Например, если известно точное значение высоты коньковой части, то определяется угол наклона по первой формуле. Найти угол можно будет по таблице тангенсов. Если же в основе расчетов лежит угол кровли, то найти параметр высоты конька можно по третьей формуле. Длину стропил, имея значение угла наклона и параметров катетов, можно посчитать по четвертой формуле.
Таблица тангенсов
Как зависят габариты мансарды от угла наклона?
Чтобы появилась возможность полезно использовать чердачное помещение, стоит задуматься о строительстве мансарды. И здесь угол наклона кровли приобретает так называемое прикладное значение. В зависимости от того, каким будет это значение, зависит и свободное пространство чердачного помещения. Так, чем меньше значение угла наклона, тем меньше свободного места будет в этой части дома.
Важно! Высота потолка в мансарде не может быть менее 2 м.
Угол наклона крыши
Таким образом, мансарду надо строить только с крутыми скатами. Но в этом случае выявляются определенные проблемы: размеры кровли увеличиваются, высота стропильной конструкции – тоже, появится необходимость проектирования массы нужных мелких элементов. Такая кровля станет сильнее «парусить» и должна быть очень прочной, чтобы выдержать различные воздействия внешних факторов.
Расчет угла наклона
Для того, что произвести корректные расчёты можно воспользоваться специальными интернет-онлайн сервисами. С их помощью можно практически безошибочно подобрать необходимые параметры и исключить ошибки при возведении.
Надо отметить, что при расчёте необходимых параметров должны обязательно учитываться следующие величины:
- длина стропил;
- высота будущего конька крыши;
- длина пролёта одного ската крыши;
- тангенс угла наклона.
Учитывая все эти параметры можно сделать однозначный вывод о том, что чем меньше высота будущей крыши, тем соответственно меньше должна быть длина ската кровли двускатной крыши.
Неправильно выбранный угол наклона, к сожалению, может неимоверно сократить максимальный срок эксплуатации кровли.
Значения снеговой нагрузки
Россия – страна огромная, и климат в разных ее точках может существенно отличаться друг от друга. Показатели снеговой нагрузки – тоже. Существует 8 основных зон, разделенных по интенсивности снеговой нагрузки.
Карта распределения зон по снеговой нагрузке
Для расчета снеговой нагрузки на проектируемое строение используется формула Рсн = Рст.н х m, где Рст.н. – показатель, определяемый по специальным таблицам, а m – коэффициент поправки, который зависит от угла ската кровли. Он будет равен 1, если угол ската варьируется в пределах 0-25 градусов, 0,7 – при скатах 25-60 градусов. Если угол превышает 60 градусов, то снеговая нагрузка при проектировании крыши не учитывается.
Зональное распределение по среднему значению снеговой нагрузки
Расчет неравномерной нагрузки на четырехскатную крышу
Цены на снегозадержатели
Снегозадержатель
Значения ветровой нагрузки
Так как ветер может менять направление движения, выявить ветровую нагрузку будет гораздо сложнее, чем снеговую. Кровля благодаря ему может прижиматься к основанию, но также может подвергаться действию определенной силы, которая будет стремиться сорвать ее с дома. Также ветер действует на все строение неравномерно.
Для проведения нужных расчетов придется использовать только превалирующее направление ветра в данном регионе, которое определяется по «розе ветров». Также при расчетах требуется учитывать наличие вблизи зданий, гор, лесов и других элементов, которые могут не только менять направление ветра, но и в некоторой степени регулировать его силу, защищая строение от шквалов.
Распределение зон по ветровой нагрузке
Согласно карте можно выявить основные ветровые характеристики, превалирующие в определенной зоне страны. Далее определяется ветровое давление Рвт (кг/м2). Оно будет меняться в зависимости от зоны:
- Ia – 24;
- I – 32;
- II – 42;
- III – 53;
- IV – 67;
- V – 84;
- VI – 100;
- VII – 120.
Затем используется формула Рв = Рвт х К х С, где К – значение коэффициента, зависящего от высоты строения и особенностей местности, а С – коэффициент, зависящий от угла наклона ската и направления ветра.
Таблица. Определение коэффициента К.
| Высота строения, м | А | Б | В |
| Менее 5 | 0,75 | 0,5 | 0,4 |
| 5-10 | 1 | 0,65 | 0,4 |
| 10-20 | 1,25 | 0,85 | 0,55 |
| 20-40 | 1,5 | 1,1 | 0,8 |
Ветровая нагрузка
А, Б, В – это определенные типы зон, А – открытая голая местность, где ветровая нагрузка будет максимальной, зона Б относится к небольшим жилым поселкам с высотой препятствий до 10 м, пересеченной местности или окруженной лесами территории, а В – это зона плотной застройки в городах, где высота зданий составляет 25 и более метров.
На заметку! Определить, какую зону выбрать в каждом конкретном случае, поможет значение высоты здания Н, которая умножается на 30. Таким образом, получается подходящий радиус зоны. Например, при высоте строения 60 м ориентироваться стоит на окружность с радиусом 2 км.
Распределение крыши здания на зоны при подсчете ветровой нагрузки
Согласно приведенному выше рисунку, большое значение при определении воздействия ветра на определенный участок кровли имеет показатель е. Он будет равен 2хН или b (выбирается тот, что меньше). Коэффициент с определяется по таблице с учетом угла наклона кровельных скатов.
Таблица. Значение С (фронтон).
| Угол ската | G | F | I | H |
| 0 | -1,3 | -1,8 | -0,5 | -0,7 |
| 15 | -1,3 | -1,3 | -0,5 | -0,6 |
| 30 | -1,4 | -1,1 | -0,5 | -0,8 |
| 45 | -1,4 | -1,1 | -0,5 | -0,9 |
| 60 | -1,2 | -1,1 | -0,5 | -0,8 |
Таблица. Значение С (скат).
| Угол ската | G | F | I | H | J |
| 15 | -0,8 или 0,2 | -0,9 или 0,2 | -0,4 | -0,3 или 0,2 | -1 |
| 30 | -0,5 или 0,7 | -0,5 или 0,7 | -0,4 | -0,2 или 0,4 | -0,5 |
| 45 | 0,7 | 0,7 | -0,2 | 0,6 | -0,3 |
| 60 | 0,7 | 0,7 | -0,2 | 0,7 | -0,3 |
Суммарное силовое воздействие на каждый участок кровли вычисляется по формуле: Рсум = Рсн + Рв. Этот показатель станет исходным для расчета стропил.
На заметку! Проще всего произвести расчеты угла ската не самостоятельно, а с использованием онлайн-калькуляторов либо компьютерных программ.
Как рассчитать угол наклона крыши: используем калькулятор
Проекты возводимых загородных особняков могут учитывать множество требований, пожеланий и даже причуд или «капризов» их владельцев владельца. Но всегда их «роднит» общая особенность — без надежной крыши никогда не обходится ни одно их зданий. И в этом вопросе на первый план должны выходить не столько архитектурные изыски заказчика, сколько специфические требования к этому элементу строения. Это надежность и устойчивость всей стропильной системы и кровельного покрытия, полноценное выполнение крышей своего прямого предназначения – защиты от проникновения влаги (а в ряде случаев, кроме того, еще и термо- и звукоизоляции), при необходимости – функциональность расположенных непосредственно под кровлей помещений.
Как рассчитать угол наклона крыши
Проектирование конструкции крыши – дело чрезвычайно ответственное и достаточно непростое, особенно при сложных ее конфигурациях. Разумнее всего будет доверить это дело профессионалам, которое владеют методикой проведения необходимых расчетов и соответствующим программным обеспечение для этого. Однако, владельцу дома тоже могут быть интересны некоторые теоретические моменты. Например, немаловажно знать, как рассчитать угол наклона крыши самостоятельно, хотя бы приблизительно — для начала.
Это даст возможность сразу прикинуть возможность реализации своих «авторских прикидок» — по соответствию задуманного реальным условиям региона, по «архитектуре» самой крыши, по планируемому кровельному материалу, по использованию чердачного помещения. В определенной степени рассчитанный угол ската кровли поможет провести предварительный подсчет параметров и количества пиломатериалов для стропильной системы, общей площади кровельного покрытия.
В каких величинах удобнее измерять угол ската крыши?
Казалось бы – совершенно излишний вопрос, так как все со школьной скамьи знают, что угол измеряется в градусах. Но ясность здесь все же нужна, потому что и в технической литературе, и в справочных таблицах, и в привычном обиходе некоторых опытных мастеров нередко встречаются и иные единицы измерения – проценты или же относительные соотношения сторон.
И еще одно необходимое уточнение — что принимается за угол наклона крыши?
Что же понимается под углом наклона крыши?
Угол наклона – это угол, образованный пересечением двух плоскостей: горизонтальной и плоскостью ската кровли. На рисунке он показан буквой греческого алфавита α.
Интересующие нас острые углы (тупоугольных скатов не может быть просто по определению), лежит в диапазоне от 0 до 90°. Скаты круче 50 ÷ 60 ° в «чистом» виде встречаются чрезвычайно редко и то, как правило, для декоративного оформления крыш – при строительстве остроконечных башенок в готическом стиле. Однако есть и исключение – такими крутыми могут быть скаты нижнего ряда стропил крыши мансардного типа.
Нижние стропила крыши мансардного типа могут располагаться под очень большим углом
И все же чаще всего приходится иметь дело со скатами, лежащим в диапазоне от 0 до 45°
С градусами понятно – все, наверное, представляют транспортир с его делениями. А ка быть с другими единицами измерения?
Тоже ничего сложного.
Относительное соотношение сторон – это максимально упрощенная дробь, показывающая отношение высоты подъёма ската (на рисунке выше обозначена латинской Н) к проекции ската крыши на горизонтальную плоскость (на схеме – L).
L – это может быть, в зависимости от конструкции крыши, половина пролета (при симметричной двускатной крыше), пролет полностью (если крыша односкатная), либо, при сложных конфигурациях кровли, действительно линейный участок, определяемый проведенной к горизонтальной плоскости проекцией. Например, на схеме мансардной крыши такой участок хорошо показан – по горизонтальной балке от самого угла до вертикальной стойки, проходящей от верхней точки нижнего стропила.
Угол уклона так и записывается, дробью, например «1 : 3».
Однако, на практике нередко случается так, что использовать величину угла уклона в таком представлении будет чрезвычайно неудобен, если, скажем, числа в дроби получаются некруглые и несокращаемые. Например, мало что скажет неопытному строителю соотношение 3 : 11. На этот случай есть возможность воспользоваться еще одной величиной измерения уклона крыши – процентами.
Находится эта величина чрезвычайно просто – необходимо просто найти результат деления уже упомянутой дроби, а затем умножить его на 100. Например, в приведенном выше примере 3 : 11
3 : 11 = 0,2727 × 100 = 27,27 %
Итак, получена величина уклона ската кровли, выраженная в процентах.
А что делать, если требуется перейти от градусов к процентам или наоборот?
Можно запомнить такое соотношение. 100 % — это угол 45 градусов, когда катеты прямоугольного треугольника равны между собой, то есть в нашем случае высота ската равна длине его горизонтальной проекции.
В таком случае, 45° / 100 = 0,45° = 27´. Один процент уклона равен 27 угловым минутам.
Если подойти с другой стороны, то 100 / 45° = 2,22 %. То есть получаем, что один градус – это 2, 22% уклона.
Для простоты перевода величин из одних в другие можно воспользоваться таблицей:
| Значение в градусах | Значение в % | Значение в градусах | Значение в % | Значение в градусах | Значение в % |
| 1° | 2,22% | 16° | 35,55% | 31° | 68,88% |
| 2° | 4,44% | 17° | 37,77% | 32° | 71,11% |
| 3° | 6,66% | 18° | 40,00% | 33° | 73,33% |
| 4° | 8,88% | 19° | 42,22% | 34° | 75,55% |
| 5° | 11,11% | 20° | 44,44% | 35° | 77,77% |
| 6° | 13,33% | 21° | 46,66% | 36° | 80,00% |
| 7° | 15,55% | 22° | 48,88% | 37° | 82,22% |
| 8° | 17,77% | 23° | 51,11% | 38° | 84,44% |
| 9° | 20,00% | 24° | 53,33% | 39° | 86,66% |
| 10° | 22,22% | 25° | 55,55% | 40° | 88,88% |
| 11° | 24,44% | 26° | 57,77% | 41° | 91,11% |
| 12° | 26,66% | 27° | 60,00% | 42° | 93,33% |
| 13° | 28,88% | 28° | 62,22% | 43° | 95,55% |
| 14° | 31,11% | 29° | 64,44% | 44° | 97,77% |
| 15° | 33,33% | 30° | 66,66% | 45° | 100,00% |
Для наглядности будет полезным привести графическую схему, которая очень доступно показывает взаимосвязь всех упомянутых линейных параметров с углом ската и величинами его измерения.
Схема А. Взаимозависимость единиц измерения угла наклона крыши и допустимые типы кровли
К этому рисунку еще предстоит вернуться, когда будут рассматриваться виды кровельных покрытий.
Еще проще будет рассчитать крутизну и угол наклона ската. если воспользоваться встроенным калькулятором, размещенным ниже:
Калькулятор расчета крутизны ската по известному значению высоты конька
Перейти к расчётам
Зависимость типа кровельного покрытия от крутизны ската
Планируя постройку собственного дома, хозяин участка наверняка уже проводит «прикидку» и своей голове, и с членами семьи – как будет выглядеть их будущее жилье. Кровля в этом вопросе, безусловно, занимает одно из первостепенных значений. И вот здесь необходимо учитывать то, что далеко не всякий кровельный материал может использоваться на различных по крутизне скатах крыш. Чтобы не возникало недоразумений позднее, необходим заранее предусматривать эту взаимосвязь.
Диаграмма распределения крыш по крутизне ската
Крыши по углу наклона ската можно условно разделит на плоские (уклон до 5°), с малым уклоном (от 6 до 30°) и крутоуклонные, соответственно, с углом ската более 30°.
У каждого из типов крыш есть свои достоинства и недостатки. Например, плоские крыши имеют минимальную площадь, но потребуют особых мер гидроизоляции. На крутых крышах не задерживаются снежные массы, однако они больше подвержены ветровой нагрузке из-за своей «парусности». Так и кровельный материал – в силу собственных технологических или эксплуатационных особенностей имеет определенные ограничения на применения с разными уклонами скатов.
Обратимся к уже рассматриваемому ранее рисунку (схема A). Черными кружками с дугообразными стрелками и синими цифрами обозначены области применения различных кровельных покрытий (острие стрелки указывает на минимально допустимое значение крутизны ската):
1 – это дранка, щепа, натуральный гонт. В этой же области лежит и применение до сих пор используемых в южных краях камышовых кровель.
2 – натуральное штучное черепичное покрытие, битумно-полимерные плитки, сланцевые плитки.
3 – рулонные материалы на битумной основе, не менее четырёх слоев, с внешней гравийной посыпкой, утопленной в слой расплавленной мастики.
4 – аналогично пункту 3, но для надёжности кровли достаточно трех слоев рулонного материала.
5 – аналогичные вышеописанным рулонные материалы (не менее трех слоев), но без наружной защитной гравийной посыпки.
6 – рулонные кровельные материалы, наклеиваемые на горячую мастику не менее, чем в два слоя. Металлочерепица, профнастил.
7 – волнистые асбестоцементные листы (шифер) унифицированного профиля.
8 – черепичное глиняное покрытие
9 – асбестоцементные листы усиленного профиля.
10 – кровельная листовая сталь с развальцовкой соединений.
11 – шиферное покрытие обычного профиля.
Таким образом, если есть желание покрыть крышу кровельным материалом определенного типа, угол уклона ската должен планироваться в указанных рамках.
Зависимость высоты конька от угла наклона крыши
Для тех читателей, которые хорошо помнят курс тригонометрии средней школы, этот раздел может показаться неинтересным. Они могут сразу его пропустить и перейти дальше. А вот подзабывшим это нужно освежить знания о взаимозависимости углов и сторон в прямоугольном треугольнике.
Для чего это надо? В рассматриваемом случае возведения крыши всегда в расчетах отталкиваются от прямоугольного треугольника. Два его катета – это длина проекции ската на горизонтальную плоскость (длина пролета, половины пролета и т.п. – в зависимости от типа крыши) и высота ската в высшей точке (на коньке или при переходе на верхние стропила – при расчете нижних стропил мансардной крыши). Понятно, что постоянная величина здесь одна – это длина пролета. А вот высоту можно изменять, варьируя угол наклона крыши.
В таблице приведены две основные зависимости, выраженные через тангенс и синус угла наклона ската. Существуют и иные зависимости (через косинус или котангенс) но в данном случае нам достаточно этих двух тригонометрических функций.
| Графическая схема | Основные тригонометрические соотношения | |
| Н — высота конька | ||
| S — длина ската крыши | ||
| L — половина длины пролета (при симметричной двускатной крыше) или длина пролета (при односкатной крыше) | ||
| α — угол ската крыши | ||
| tg α = H / L | Н = L × tg α | |
| sin α = H / S | S = H / sin α | |
Зная эти тригонометрические тождества, можно решить практически все задачи по предварительному проектированию стропильной конструкции.
Для наглядности — треугольник в приложении к крыше дома
Так, если необходимо «плясать» от четко установленной высоты подъёма конька, то отношением tg α = H / L несложно будет определить угол.
По полученному делением числу в таблице тангенсов находят угол в градусах. Тригонометрические функции часто бывают заложены в инженерные калькуляторы, они есть в обязательном порядке в таблицах Exel (для тех, кто умеет работать с этим удобным приложением. Правда, там расчет ведется не в градусах, а в радианах). Но чтобы нашему читателю не приходилось отвлекаться на поиски нужных таблиц, приведем значение тангенсов в диапазоне от 1 до 80°.
| Угол | Значение тангенса | Угол | Значение тангенса | Угол | Значение тангенса | Угол | Значение тангенса |
| tg(1°) | 0.01746 | tg(21°) | 0.38386 | tg(41°) | 0.86929 | tg(61°) | 1.80405 |
| tg(2°) | 0.03492 | tg(22°) | 0.40403 | tg(42°) | 0.9004 | tg(62°) | 1.88073 |
| tg(3°) | 0.05241 | tg(23°) | 0.42447 | tg(43°) | 0.93252 | tg(63°) | 1.96261 |
| tg(4°) | 0.06993 | tg(24°) | 0.44523 | tg(44°) | 0.96569 | tg(64°) | 2.0503 |
| tg(5°) | 0.08749 | tg(25°) | 0.46631 | tg(45°) | 1 | tg(65°) | 2.14451 |
| tg(6°) | 0.1051 | tg(26°) | 0.48773 | tg(46°) | 1.03553 | tg(66°) | 2.24604 |
| tg(7°) | 0.12278 | tg(27°) | 0.50953 | tg(47°) | 1.07237 | tg(67°) | 2.35585 |
| tg(8°) | 0.14054 | tg(28°) | 0.53171 | tg(48°) | 1.11061 | tg(68°) | 2.47509 |
| tg(9°) | 0.15838 | tg(29°) | 0.55431 | tg(49°) | 1.15037 | tg(69°) | 2.60509 |
| tg(10°) | 0.17633 | tg(30°) | 0.57735 | tg(50°) | 1.19175 | tg(70°) | 2.74748 |
| tg(11°) | 0.19438 | tg(31°) | 0.60086 | tg(51°) | 1.2349 | tg(71°) | 2.90421 |
| tg(12°) | 0.21256 | tg(32°) | 0.62487 | tg(52°) | 1.27994 | tg(72°) | 3.07768 |
| tg(13°) | 0.23087 | tg(33°) | 0.64941 | tg(53°) | 1.32704 | tg(73°) | 3.27085 |
| tg(14°) | 0.24933 | tg(34°) | 0.67451 | tg(54°) | 1.37638 | tg(74°) | 3.48741 |
| tg(15°) | 0.26795 | tg(35°) | 0.70021 | tg(55°) | 1.42815 | tg(75°) | 3.73205 |
| tg(16°) | 0.28675 | tg(36°) | 0.72654 | tg(56°) | 1.48256 | tg(76°) | 4.01078 |
| tg(17°) | 0.30573 | tg(37°) | 0.75355 | tg(57°) | 1.53986 | tg(77°) | 4.33148 |
| tg(18°) | 0.32492 | tg(38°) | 0.78129 | tg(58°) | 1.60033 | tg(78°) | 4.70463 |
| tg(19°) | 0.34433 | tg(39°) | 0.80978 | tg(59°) | 1.66428 | tg(79°) | 5.14455 |
| tg(20°) | 0.36397 | tg(40°) | 0.8391 | tg(60°) | 1.73205 | tg(80°) | 5.67128 |
В случае, наоборот, когда за основу берется угол наклона кровли, высота расположения конька определяется по обратной формуле:
H = L × tg α
Теперь, имея значения двух катетов и угла наклона кровли, очень просто вычислить и требуемую длину стропила от конька до карнизного свеса. Можно применить теорему Пифагора
S = √ (L² + H²)
Или же, что, наверное, проще, так как уже известна величина угла, применить тригонометрическую зависимость:
S = H / sin α
Значение синусов углов — в таблице ниже.
| Угол | Значение синуса | Угол | Значение синуса | Угол | Значение синуса | Угол | Значение синуса |
| sin(1°) | 0.017452 | sin(21°) | 0.358368 | sin(41°) | 0.656059 | sin(61°) | 0.87462 |
| sin(2°) | 0.034899 | sin(22°) | 0.374607 | sin(42°) | 0.669131 | sin(62°) | 0.882948 |
| sin(3°) | 0.052336 | sin(23°) | 0.390731 | sin(43°) | 0.681998 | sin(63°) | 0.891007 |
| sin(4°) | 0.069756 | sin(24°) | 0.406737 | sin(44°) | 0.694658 | sin(64°) | 0.898794 |
| sin(5°) | 0.087156 | sin(25°) | 0.422618 | sin(45°) | 0.707107 | sin(65°) | 0.906308 |
| sin(6°) | 0.104528 | sin(26°) | 0.438371 | sin(46°) | 0.71934 | sin(66°) | 0.913545 |
| sin(7°) | 0.121869 | sin(27°) | 0.45399 | sin(47°) | 0.731354 | sin(67°) | 0.920505 |
| sin(8°) | 0.139173 | sin(28°) | 0.469472 | sin(48°) | 0.743145 | sin(68°) | 0.927184 |
| sin(9°) | 0.156434 | sin(29°) | 0.48481 | sin(49°) | 0.75471 | sin(69°) | 0.93358 |
| sin(10°) | 0.173648 | sin(30°) | 0.5 | sin(50°) | 0.766044 | sin(70°) | 0.939693 |
| sin(11°) | 0.190809 | sin(31°) | 0.515038 | sin(51°) | 0.777146 | sin(71°) | 0.945519 |
| sin(12°) | 0.207912 | sin(32°) | 0.529919 | sin(52°) | 0.788011 | sin(72°) | 0.951057 |
| sin(13°) | 0.224951 | sin(33°) | 0.544639 | sin(53°) | 0.798636 | sin(73°) | 0.956305 |
| sin(14°) | 0.241922 | sin(34°) | 0.559193 | sin(54°) | 0.809017 | sin(74°) | 0.961262 |
| sin(15°) | 0.258819 | sin(35°) | 0.573576 | sin(55°) | 0.819152 | sin(75°) | 0.965926 |
| sin(16°) | 0.275637 | sin(36°) | 0.587785 | sin(56°) | 0.829038 | sin(76°) | 0.970296 |
| sin(17°) | 0.292372 | sin(37°) | 0.601815 | sin(57°) | 0.838671 | sin(77°) | 0.97437 |
| sin(18°) | 0.309017 | sin(38°) | 0.615661 | sin(58°) | 0.848048 | sin(78°) | 0.978148 |
| sin(19°) | 0.325568 | sin(39°) | 0.62932 | sin(59°) | 0.857167 | sin(79°) | 0.981627 |
| sin(20°) | 0.34202 | sin(40°) | 0.642788 | sin(60°) | 0.866025 | sin(80°) | 0.984808 |
Для тех же читателей, кто просто не хочет погружаться в самостоятельные тригонометрические расчеты, рекомендуем встроенный калькулятор, который быстро и точно определит длину ската кровли (без учета карнизного свеса) по имеющимся значениям высоты конька и длины горизонтальной проекции ската.
Калькулятор расчета длины ската кровли по известному значению высоты конька
Умелое использование тригонометрических формул позволяет, при нормальном пространственном воображении и при умении выполнять несложные чертежи, провести расчеты и более сложным по конструкции крыш.
Опираясь на базовые соотношения, несложно разделить на треугольники и рассчитать вальмовую крышу
Например, даже кажущуюся такой «навороченной» вальмовую или мансардную крышу можно разбить на совокупности треугольников, а затем последовательно просчитать все необходимые размеры.
Зависимость размеров помещения мансарды от угла наклона скатов крыши
Если хозяевами будущего дома планируется использовать чердак в качестве функционального помещения, иначе говоря – сделать мансарду, то определение угла ската крыши приобретает вполне прикладное значение.
Чем больше угол уклона — тем просторнее мансарда
Много объяснять здесь ничего не надо – приведённая схема наглядно показывает, что чем меньше угол наклона, тем теснее свободное пространство в чердачном помещении.
Чтобы стало несколько понятнее, лучше выполнить подобную схему в определенном масштабе. Вот, например, как будет выглядеть мансардное помещение в доме с шириной фронтонной части 10 метров. Следует учитывать, что высота потолка никак не может быть ниже 2 метров. (Откровенно говоря, и двух метров маловато для жилого помещения– потолок будет неизбежно «давить» на человека. Обычно исходят из высоты хотя-бы 2.5 метра).
Для образца — масштабированная схема мансарды
Можно привести уже подсчитанные средние значения получаемой в мансарде комнаты, в зависимости от угла наклона обычной двускатной крыши. Кроме того, в таблице приведены величины длины стропил и площади кровельного материала с учетом 0,5 метров карнизного свеса кровли.
| Угол ската крыши | Высота конька | Длина ската | Полезная площадь мансардного помещения на 1 метр длины здания (при высоте потолка 2 м) | Площадь кровельного покрытия на 1 метр длины здания |
| 20 | 1.82 | 5.32 | нет | 11.64 |
| 25 | 2.33 | 5.52 | 0.92 | 12.03 |
| 30 | 2.89 | 5.77 | 2.61 | 12.55 |
| 35 | 3.50 | 6.10 | 3.80 | 13.21 |
| 40 | 4.20 | 6.53 | 4.75 | 14.05 |
| 45 | 5.00 | 7.07 | 5.52 | 15.14 |
| 50 | 5.96 | 7.78 | 6.16 | 16.56 |
Итак, чем круче наклон скатов, тем просторнее помещение. Однако, это сразу отзывается резким увеличением высоты стропильной конструкции, возрастанием размеров, а стало быть – и массы деталей для ее монтажа. Гораздо больше потребуется и кровельного материала – площадь покрытия также быстро растет. Плюс к этому, нельзя забывать и о возрастании эффекта «парусности» — большей подверженности ветровой нагрузке. Видам внешних нагрузок будет посвящена последняя глава настоящей публикации.
Для сравнения — крыша мансардного типа дает выигрыш по полезному пространству даже при меньшей высоте
Чтобы в определенной степени нивелировать подобные негативные последствия, проектировщики и строители часто применяют особую конструкцию мансардной крыши – о ней уже упоминалось в настоящей статье. Она сложнее в расчетах и изготовлении, но дает существенный выигрыш в получаемой полезной площади мансардного помещения с уменьшением общей высоты здания.
Зависимость величины внешних нагрузок от угла наклона крыши
Еще одно важнейшее прикладное применение рассчитанного значения угла наклона кровли – это определение степени его влияния на уровень внешних нагрузок, выпадающих на конструкцию крыши.
Здесь прослеживается интересная взаимосвязь. Можно заранее рассчитать все параметры – углы и линейные размеры, но всегда в итоге приходят к деталировке. То есть необходимо определить, из какого материала будут изготавливаться детали и узлы стропильной системы, какова должна быть их площадь сечения, шаг расположения, максимальная длина между соседними точками опоры, способы крепления элементов между собой и к несущим стенам здания и многое другое.
Вот здесь на первый план выходят нагрузки, которые испытывает конструкция крыши. Помимо собственного веса, огромное значение имеют внешние воздействия. Если не брать в расчет несвойственные для наших краев сейсмические нагрузки, то главным образом надо сосредоточится на снеговой и ветровой. Величина обеих – напрямую связана с углом расположения кровли к горизонту.
Снеговая нагрузка
Понятно, что на огромной территории Российской Федерации среднестатистическое количество выпадаемых в виде снега осадков существенно различается по регионам. По результатам многолетних наблюдений и вычислений, составлена карта территории страны, на которой указаны восемь различных зон по уровню снеговой нагрузки.
Карта распределения зон на территории РФ по снеговой нагрузке
Восьмая, последняя зона – это некоторые малозаселенные районы Дальнего Востока, и ее можно особо не рассматривать. Значения же для других зон – указаны в таблице
| Зональное распределение территории РФ по среднему значению снеговой нагрузки | Значение в кПа | Значение в кг/м² |
| I | 0.8 кПа | 80 кг/м² |
| II | 1.2 кПа | 120 кг/м² |
| III | 1.8 кПа | 180 кг/м² |
| IV | 2.4 кПа | 240 кг/м² |
| V | 3.2 кПа | 320 кг/м² |
| VI | 4.0 кПа | 400 кг/м² |
| VII | 4.8 кПа | 480 кг/м² |
Теперь, чтобы рассчитать конкретную нагрузку для планируемого здания, необходимо воспользоваться формулой:
Рсн = Рсн.т × μ
Рсн.т – значение, которое мы нашли с помощью карты и таблицы;
Μ – поправочный коэффициент, который зависит от угла ската α
- при α от 0 до 25° — μ=1
- при α более 25 и до 60° — μ=0,7
- при α более 60° снеговую нагрузку в расчет не принимают, так как снег не должен удерживаться на плоскости скатов кровли.
Например, дом возводится в Башкирии. Планируемая скатов его крыши – 35°.
Находим по таблице – зона V, табличное значение — Рсн.т = 3,2 кПа
Находим итоговое значение Рсн = 3.2 × 0,7 = 2,24 кПа
(если значение нужно в килограммах на квадратный метр, то используется соотношение
1 кПа ≈ 100 кг/м²
В нашем случае получается 224 кг/м².
Ветровая нагрузка
С ветровой нагрузкой все обстоит намного сложнее. Дело в том, что она может быть разнонаправленной – ветер способен оказывать давление на крышу, прижимая ее к основанию, но вместе с тем возникают аэродинамические «подъемные» силы, стремящиеся оторвать кровлю от стен.
Кроме того, ветровая нагрузка воздействует на разные участки крыши неравномерно, поэтому знать только среднестатистический уровень ветровой нагрузки – недостаточно. В расчет принимаются господствующие направления ветров в данной местности («роза ветров»), степень насыщенности участка местности препятствиями для распространения ветра, высота здания и окружающих его строений, другие критерии.
Примерный порядок подсчета ветровой нагрузки выглядит следующим образом.
В первую очередь, по аналогии с ранее проведёнными расчетами, на карте определяется регион РФ и соответствующая ему зона.
Распределение зон на территории РФ по уровню ветрового давления
Далее, по таблице можно определить среднее для конкретного региона значение ветрового давления Рвт
| Региональное распределение территории РФ по уровню средней ветровой нагрузки | Iа | I | II | III | IV | V | VI | VII |
| Табличное значение ветрового давления, кг/м ² (Рв) | 24 | 32 | 42 | 53 | 67 | 84 | 100 | 120 |
Далее расчет проводится по следующей формуле:
Рв = Рвт × k × c
Рвт – табличное значение ветрового давления
k – коэффициент, учитывающий высоту здания и характер местности вокруг него. Определяют его по таблице:
| Высота возводимого здания (сооружения) (z) | Зона А | Зона Б | Зона В |
| не более 5 м | 0.75 | 0.5 | 0.4 |
| от 5 до 10 м | 1.0 | 0.65 | 0.4 |
| от 10 до 20 м | 1.25 | 0.85 | 0.55 |
| от 20 до 40 м | 1.5 | 1.1 | 0.8 |
В таблице указаны три различные зоны:
- Зона «А» — открытая «голая» местность, например, степь, пустыня, тундра или лесотундра, полностью открытые ветровому воздействию побережья морей и океанов, крупных озер, рек, водохранилищ.
- Зона «Б» — территории жилых поселков, небольших городов, лесистые и пересеченные участки местности, с препятствиями для ветра, естественными или искусственными, высотой порядка 10 метров.
- Зона «В» — территории крупных городов с плотной застройкой, со средней высотой зданий 25 метров и выше.
Дом считается соответствующим именно этой зоне, если указанные характерные особенности расположены в радиусе не менее, чем высота здания h, умноженная на 30 (например, для дома 12 м радиус зоны должен быть не мене 360 м). При высоте здания выше 60 м принимается окружность радиусом 2000 м.
c – а вот это – тот самый коэффициент, который и зависит от направления ветра на здание и от угла наклона крыши.
Как уже упоминалось, в зависимости от направления воздействия и особенностей крыши ветер может давать разнонаправленные векторы нагрузки. На схеме ниже приведены зоны ветрового воздействия, на которые обычно делится площадь крыши.
Распределение крыши здания на зоны при подсчете ветровой нагрузки
Обратите внимание – фигурирует промежуточная вспомогательная величина е. Ее принимают равной либо 2 × h, либо b, в зависимости от направления ветра. В любом случае, из двух значений берут то, что будет меньше.
Коэффициент с для каждой из зон берут из таблиц, в который учтен угол уклона кровли. Если для одного участка предусмотрены и положительное и отрицательное значения коэффициента, то проводятся оба вычисления, а затем данные суммируются.
Таблица коэффициента «с» для ветра, направленного в скат кровли
| Угол ската кровли ( α) | F | G | H | I | J |
| 15 ° | — 0,9 | -0.8 | — 0.3 | -0.4 | -1.0 |
| 0.2 | 0.2 | 0.2 | |||
| 30 ° | -0.5 | -0.5 | -0.2 | -0.4 | -0.5 |
| 0.7 | 0.7 | 0.4 | |||
| 45 ° | 0.7 | 0.7 | 0.6 | -0.2 | -0.3 |
| 60 ° | 0.7 | 0.7 | 0.7 | -0.2 | -0.3 |
| 75 ° | 0.8 | 0.8 | 0.8 | -0.2 | -0.3 |
Таблица коэффициента «с» для ветра, направленного во фронтонную часть
| Угол ската кровли ( α) | F | G | H | I |
| 0 ° | -1.8 | -1.3 | -0.7 | -0.5 |
| 15 ° | -1.3 | -1.3 | -0.6 | -0.5 |
| 30 ° | -1.1 | -1.4 | -0.8 | -0.5 |
| 45 ° | -1.1 | -1.4 | -0.9 | -0.5 |
| 60 ° | -1.1 | -1.2 | -0.8 | -0.5 |
| 75 ° | -1.1 | -1.2 | -0.8 | -0.5 |
Вот теперь то, подсчитав ветровую нагрузку, можно будет определить суммарное внешнее силовое воздействие для каждого участка крыши.
Рсум = Рсн + Рв
Полученное значение становится исходной величиной для определения параметров стропильной системы. В частности, в таблице, приведенной ниже, можно найти значения допустимой свободной длины стропил между точками опоры, в зависимости от сечения бруса, расстояния между стропилами, сорта материала (древесины хвойных пород) и, соответственно, уровня суммарной ветровой и снежной нагрузки.
| Сорт древесины | Сечение стропил (мм) | Расстояние между соседними стропилами (мм) | |||||
| 300 | 400 | 600 | 300 | 400 | 600 | ||
| суммарная нагрузка (снеговая + ветровая) | 1.0 кПа | 1.5 кПа | |||||
| Древесина высшего сорта | 40×89 | 3.22 | 2.92 | 2.55 | 2.81 | 2.55 | 2.23 |
| 40×140 | 5.06 | 4.60 | 4.02 | 4.42 | 4.02 | 3.54 | |
| 50×184 | 6.65 | 6.05 | 5.28 | 5.81 | 5.28 | 4.61 | |
| 50×235 | 8.50 | 7.72 | 6.74 | 7.42 | 6.74 | 5.89 | |
| 50×286 | 10.34 | 9.40 | 8.21 | 9.03 | 8.21 | 7.17 | |
| I или II сорт | 40×89 | 3.11 | 2.83 | 2.47 | 2.72 | 2.47 | 2.16 |
| 40×140 | 4.90 | 4.45 | 3.89 | 4.28 | 3.89 | 3.40 | |
| 50×184 | 6.44 | 5.85 | 5.11 | 5.62 | 5.11 | 4.41 | |
| 50×235 | 8.22 | 7.47 | 6.50 | 7.18 | 6.52 | 5.39 | |
| 50×286 | 10.00 | 9.06 | 7.40 | 8.74 | 7.66 | 6.25 | |
| III сорт | 40×89 | 3.06 | 2.78 | 2.31 | 2.67 | 2.39 | 1.95 |
| 40×140 | 4.67 | 4.04 | 3.30 | 3.95 | 3.42 | 2.79 | |
| 50×184 | 5.68 | 4.92 | 4.02 | 4.80 | 4.16 | 3.40 | |
| 50×235 | 6.95 | 6.02 | 4.91 | 5.87 | 5.08 | 4.15 | |
| 50×286 | 8.06 | 6.98 | 6.70 | 6.81 | 5.90 | 4.82 | |
| суммарная нагрузка (снеговая + ветровая) | 2.0 кПа | 2.5 кПа | |||||
| Древесина высшего сорта | 40×89 | 4.02 | 3.65 | 3.19 | 3.73 | 3.39 | 2.96 |
| 40×140 | 5.28 | 4.80 | 4.19 | 4.90 | 4.45 | 3.89 | |
| 50×184 | 6.74 | 6.13 | 5.35 | 6.26 | 5.69 | 4.97 | |
| 50×235 | 8.21 | 7.46 | 6.52 | 7.62 | 6.92 | 5.90 | |
| 50×286 | 2.47 | 2.24 | 1.96 | 2.29 | 2.08 | 1.82 | |
| I или II сорт | 40×89 | 3.89 | 3.53 | 3.08 | 3.61 | 3.28 | 2.86 |
| 40×140 | 5.11 | 4.64 | 3.89 | 4.74 | 4.31 | 3.52 | |
| 50×184 | 6.52 | 5.82 | 4.75 | 6.06 | 5.27 | 4.30 | |
| 50×235 | 7.80 | 6.76 | 5.52 | 7.06 | 6.11 | 4.99 | |
| 50×286 | 2.43 | 2.11 | 1.72 | 2.21 | 1.91 | 1.56 | |
| III сорт | 40×89 | 3.48 | 3.01 | 2.46 | 3.15 | 2.73 | 2.23 |
| 40×140 | 4.23 | 3.67 | 2.99 | 3.83 | 3.32 | 2.71 | |
| 50×184 | 5.18 | 4.48 | 3.66 | 4.68 | 4.06 | 3.31 | |
| 50×235 | 6.01 | 5.20 | 4.25 | 5.43 | 4.71 | 3.84 | |
| 50×286 | 6.52 | 5.82 | 4.75 | 6.06 | 5.27 | 4.30 | |
Понятно, что при расчете сечения стропил, шага их установки и длины пролета (расстояния межу точками опоры), берутся показатели суммарного внешнего давления для наиболее нагруженных участков кровли. Если посмотреть на схемы и значения коэффициентов таблицы, то это – G и Н.
Чтобы упростить посетителю сайта задачу по вычислению суммарной нагрузки, ниже размещен калькулятор, который рассчитает этот параметр именно для максимально нагруженных участков.
Калькулятор расчета суммарной, снеговой и ветровой нагрузки для определения необходимого сечения стропил
Перейти к расчётам
Итак, трудно преуменьшить значение правильного расчета угла наклона крыши, влияние этого параметра на целый ряд важнейших характеристик стропильной системы, да и всего здания в целом. Хотя проведение настоящих архитектурных расчетов, конечно, является в большей мере прерогативой специалистов, умение ориентироваться в основных понятиях и проводить несложные базовые вычисления – будет очень полезным для каждого грамотного владельца дома.
И в завершение статьи – видео-урок по расчету стропильной системы обычной двускатной крыши:
Видео: расчёт и монтаж двускатной стропильной системы
Вариант расчета параметров кровли с использованием калькулятора
Шаг 1. Первым делом в браузере открывается сайт, где есть онлайн-калькулятор. В данном случае можно указать массу параметров будущей кровли. Для начала выбирается форма крыши – например, односкатная.
Выбирается тип кровли
Шаг 2. Далее сайт предлагает выбрать материал, которым будет зашиваться готовая кровля (металлочерепица, шифер и т. д.).
Выбор кровельного материала
Шаг 3. Выбираются значения длины и ширины основания кровли, ориентируясь на изображение внизу страницы – там показаны определения используемых обозначений.
Выбор основных значений
Шаг 4. Сразу же можно указать и другие значения – параметры стропильной системы, вплоть до указания используемых материалов для ее сооружения. Выбирается также и значение шага обрешетки, расчет снеговой нагрузки.
Параметры стропильной системы
Шаг 5. Снеговая нагрузка определяется по региону, где будет находиться строение. Для этого есть удобная карта-схема.
Выбор региона по снеговой нагрузке
Шаг 6. Чтобы расчеты были произведены, нажимается кнопка «Рассчитать».
Нажмите кнопку «Рассчитать»
Шаг 7. В итоге на странице появится подробная таблица с указанием основных параметров кровли, в том числе и угла ее наклона.
Результаты расчетов
Также приведем примерный расчет угла кровли в зависимости от известного значения высоты конька. Для произведения расчетов следует измерить ширину фронтона (для примера это показатель будет равен 6 м). Далее это значение делится на 2 – получается 3 м. Высота конька в данном случае должна быть 1,8 м.
Теперь просто нужно воспользоваться известными из уроков геометрии формулами и узнать тангенс угла: tgA = a:b = 3:1,8 = 1,67. Значение угла по значению тангенса можно найти в таблице Брадиса. В данном случае угол ската будет равен 58-59 градусов. Его можно округлить до 60.